Паттерны это википедия – паттерн — Викисловарь

Паттерн Википедия

плитка — пример использования паттернов в дизайне помещений

Па́ттерн (англ. pattern «образец, шаблон; форма, модель; схема, диаграмма») — схема-образ, действующая как посредствующее представление, или чувственное понятие, благодаря которому в режиме одновременности восприятия и мышления выявляются закономерности, как они существуют в природе и обществе.

Паттерн понимается в этом плане как повторяющийся шаблон или образец. Элементы паттерна повторяются предсказуемо. Так, из графических паттернов складываются красивые узоры.

Каждый из органов восприятия (чувств) воспринимает паттерны в соответствии со своими особенностями.

В науке, в том числе в математике и языкознании, паттерны выявляются путём исследования.

Прямое наблюдение может выявлять визуальные паттерны, как они формируются в природе и в искусстве.
Визуальные паттерны в природе часто хаотичны. Они не копируют друг друга и часто являются фрактальными.

Паттерны в природе включают спирали, меандры, волны, пену, трещины, а также паттерны, созданные благодаря симметрии поворота и отражения. Все подобные паттерны имеют математически описываемую структуру, которая может быть выражена формулами, тем не менее математика сама по себе является поиском регулярностей, и любой конечный продукт применения функций является математическим паттерном.

Когда научные теории исследуют и предсказывают синхронно существующие регулярности в природе и обществе, то это и есть выявление паттернов.
В искусстве и архитектуре для получения определенного устойчивого воздействия декорации и различные визуальные элементы могут комбинироваться и повторяться, образуя паттерны.

В компьютерных науках шаблоны проектирования являются широко используемым решением большого класса проблем программирования.

Под паттерном в медицине понимают устойчивую комбинацию результатов исследований или других признаков (например, симптомов) при сходных жалобах пациента или у больных одной нозологии. Понятие «паттерн» включает несколько признаков (симптомов). Синдром включает один или несколько паттернов. Болезнь включает один или несколько синдромов.

Паттерны в природе[ | ]

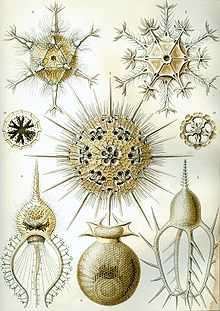рисунки морских животных Эрнста Геккеля, демонстрирующие различные виды симметрии

Ранние греческие философы, такие как Платон, Пифагор, Эмпедокл, исследовали паттерны, пытаясь объяснить порядок в природе. Современное понимание визуальных паттернов формировалось постепенно с развитием наук.

В XIX веке бельгийский физик Жозеф Плато, изучая мыльные пузыри, сформулировал концепцию минимальной поверхности. Немецкий биолог и художник Эрнст Геккель нарисовал сотни мо

ru-wiki.ru

Паттерн — Википедия

плитка — пример использования паттернов в дизайне помещений

Па́ттерн (англ. pattern «образец, шаблон; форма, модель; схема, диаграмма») — схема-образ, действующая как посредствующее представление, или чувственное понятие, благодаря которому в режиме одновременности восприятия и мышления выявляются закономерности, как они существуют в природе и обществе.

Паттерн понимается в этом плане как повторяющийся шаблон или образец. Элементы паттерна повторяются предсказуемо. Так, из графических паттернов складываются красивые узоры.

Каждый из органов восприятия (чувств) воспринимает паттерны в соответствии со своими особенностями.

В науке, в том числе в математике и языкознании, паттерны выявляются путём исследования.

Прямое наблюдение может выявлять визуальные паттерны, как они формируются в природе и в искусстве.

Визуальные паттерны в природе часто хаотичны. Они не копируют друг друга и часто являются фрактальными.

Паттерны в природе включают спирали, меандры, волны, пену, трещины, а также паттерны, созданные благодаря симметрии поворота и отражения. Все подобные паттерны имеют математически описываемую структуру, которая может быть выражена формулами, тем не менее математика сама по себе является поиском регулярностей, и любой конечный продукт применения функций является математическим паттерном.

Когда научные теории исследуют и предсказывают синхронно существующие регулярности в природе и обществе, то это и есть выявление паттернов.
В искусстве и архитектуре для получения определенного устойчивого воздействия декорации и различные визуальные элементы могут комбинироваться и повторяться, образуя паттерны.

В компьютерных науках шаблоны проектирования являются широко используемым решением большого класса проблем программирования.

Под паттерном в медицине понимают устойчивую комбинацию результатов исследований или других признаков (например, симптомов) при сходных жалобах пациента или у больных одной нозологии. Понятие «паттерн» включает несколько признаков (симптомов). Синдром включает один или несколько паттернов. Болезнь включает один или несколько синдромов.

Паттерны в природе

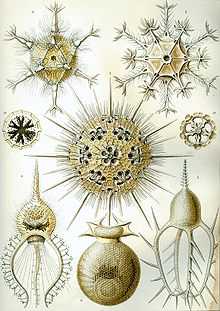рисунки морских животных Эрнста Геккеля, демонстрирующие различные виды симметрии

Ранние греческие философы, такие как Платон, Пифагор, Эмпедокл, исследовали паттерны, пытаясь объяснить порядок в природе. Современное понимание визуальных паттернов формировалось постепенно с развитием наук.

В XIX веке бельгийский физик Жозеф Плато, изучая мыльные пузыри, сформулировал концепцию минимальной поверхности. Немецкий биолог и художник Эрнст Геккель нарисовал сотни морских организмов, подчёркивая их симметрию. Шотландский биолог Дарси Томпсон первым начал изучение паттернов роста как растений, так и животных, показав, что спиральный рост можно описать простыми уравнениями. В XX веке британский математик Алан Тьюринг предсказал механизмы морфогенеза, которые ответственны за образование пятен и полос. Венгерский биолог Аристид Линденмайер и французско-американский математик Бенуа́ Мандельбро́т показали, как математика фракталов может объяснить паттерны роста растений.

Математика, физика и химия объясняют паттерны в природе на различных уровнях. Паттерны в живых организмах могут быть объяснены биологическими процессами естественного и полового отбора. Изучение формирования паттернов использует компьютерное моделирование для симуляции широкого спектра паттернов.

Видео по теме

Виды паттернов в природе

Симметрия

Симметрия для живых организмов является практически всеобщей. У большинства животных наблюдается зеркальная, или билатеральная, симметрия, она также присутствует в листьях растений и некоторых цветах, например орхидеях.

[1] Растения часто имеют круговую, или вращательную, симметрию, как у многих цветов и некоторых животных, например у медуз. Пятилучевая симметрия встречается у иглокожих, таких как морские звёзды, морские ежи и морские лилии^[2].

В неживой природе снежинка имеет красивую шестилучевую симметрию, каждая снежинка уникальна, но один и тот же паттерн повторяется на всех шести её лучах^[3]. Кристаллы обычно имеют разные виды симметрии и габитусы, они могут быть кубическими, шестигранными, восьмигранными, но настоящие кристаллы никогда не имеют пятилучевую симметрию (чего нельзя сказать о квазикристаллах).^[4]

Вращательная симметрия встречается в различных явлениях неживой природы, например при всплеске, когда капля падает в водоём,^[5] а также в сферических формах и кольцах планет, таких как Сатурн.^[6]

Деревья, фракталы

самоподобие фрактального листа

Фракталы бесконечно самоподобны.^[7][8][9] Бесконечные повторения в природе невозможны, поэтому ‘фрактальные’ паттерны фрактальны лишь приблизительно. Например, листья папоротников и зонтичных (Apiaceae) самоподобны на 2-м, 3-м или 4-м уровне. Схожие с папоротником паттерны самоподобия встречаются также у животных, включая мшанки, кораллы, гидроидные, а также в неживой природе, преимущественно в электрических разрядах.

Фракталоподобные паттерны широко встречаются в природе, в таких распространённых феноменах, как облака, речные сети, геологические разломы, горы, береговые линии,

[10] окрас животных, снежинки,^[11]кристаллы,^[12] разветвления кровеносных сосудов^[13] и морские волны.^[14]

Спирали

Спирали часто встречаются у растений и некоторых животных, преимущественно моллюсков. Например у наутилусов, головоногих моллюсков, каждая камера его раковины является приблизительной копией предыдущей камеры, увеличенной на определённый коэффициент и представленной в виде логарифмической спирали.^[15] Исходя из современного понимания фракталов, растущая спираль является частным случаем самоподобия.

[16]

Среди растений спирали образуют некоторые виды алоэ, спиралевидным является распределение листьев на стебле, а также других частей у иных растений, например: соцветья астровых, семянные головки подсолнечника или фрукты вроде ананаса^[17]:337 и салака, а также паттерн на шишках, где многочисленные спирали располагаются как по часовой, так и против часовой стрелки.

Спираль произрастания листьев может быть выведена из последовательности чисел Фибоначчи: 1, 1, 2, 3, 5, 8, 13… (каждое следующее число является суммой двух предыдущих). Например, при росте листьев из ствола, один поворот спирали равен двум листьям, поэтому паттерн или соотношение равно 1/2. У орешника соотношение 1/3; у абрикоса 2/5; у груши 3/8; у миндаля оно составляет 5/13.

[18]

Хаос, потоки, меандры

хаос в окраске ракушки Вид на Николаев из космоса. Синусоидальный паттерн, образованный реками — пример меандра

В математике динамическая система является хаотической, если она слишком чувствительна к начальным условиям (так называемый эффект бабочки^[19]).

Теория хаоса считается одним из самых важных факторов, влияющих на возникновение паттернов в природе. Существует связь между хаосом и фракталами — странные аттракторы в хаотических системах имеют фрактальную размерность.^[20]

Турбулентность в газах и жидкостях при преодолении твердого препятствия образует характерные паттерны кручения.

Меандры — это синусообразные изгибы в реках и других каналах, формируемые жидкостью, обычно водой, текущей вдоль изгибов. Если русло не является ровным, размеры и неровность изгибов увеличивается за счёт того, что течение переносит твёрдый материал, обычно песок и гальку к внутренней стороне изгиба. Внешняя часть изгиба остаётся незащищённой, поэтому эрозия усиливается, увеличивая темпы меандрирования.^[21]

Волны, дюны

Под влиянием ветра на поверхности воды и песка в природе образовываются схожие по строению хаотические паттерны, оставляющие рябь, называемые волнами на воде и дюнами на песке. Под действием ветра происходит неравномерное распределение, возвышенные участки чередуются с понижениями уровня.

Частным случаем дюн являются барханы.

Пузыри, пена

Мыльные пузыри образуют пену

Замощение

Замощение — разбиение без каких-либо накладок и без пробелов. Наиболее известным примером замощения в природе являются пчелиные соты, где шестиугольный паттерн многократно дублируется, заполняя всё пространство улья.

Трещины

Пятна и полосы

Паттерны в архитектуре

Паттерны в дизайне

Паттерны (повторяющиеся элементы) широко используются для украшения среды обитания человека — от лепнины, тротуарной плитки, обоев, паркета и кафеля до орнаментов в одежде, раскраски тканей и использования узоров в оформлении всевозможной печатной продукции. Наиболее популярные паттерны имеют имена, Клетка, Гусиные лапки, Бута, Турецкие огурцы, Алагрек, Меандр.

Паттерны часто употребляются в исламском мире. Искусствоведы подразделяют исламские узоры на стилизованные растительные, которые называются Арабеска, и геометрические, называемые Мореска.^[22]

Паттерны для детей

Простым инструментом для создания паттернов является спирограф.

Наблюдать причудливые паттерны можно с помощью калейдоскопа.

Паттерны в медицине

В медицине термин «паттерн» употребляют при анализе, например, кардиограмм, энцефалограмм и результатов других исследований, понимая под ним^[23] одинаковую последовательность колебаний биопотенциалов, повторяющуюся в одном или нескольких отведениях при одинаковых состояниях и условиях^[24]

Термин паттерн используется для обозначения последовательности нервных импульсов, имеющей определённое информационное значение^[25], например, «паттерны боли при биомеханических нарушениях суставов краниовертебрального перехода и шейного отдела позвоночника»^[26] или «паттерны двигательных и чувствительных расстройств при патологии нервных структур в дистальных отделах верхней конечности»^[27].

Паттерны широко представлены в глоссарии мануальных терапевтов (например паттерн ходьбы), рефлексотерапевтов (например, паттерн сырости-жара) и прикладных кинезиологов (например, паттерн дыхания).

Паттерны вязания

В вязании часто используются схемы рисунков, которые повторяются через определенное количество столбцов и рядов. Один такой рисунок, предназначенный для многократного повторения в вязаном изделии, и называется паттерном. Паттерн может состоять из различных видов петель, в результате получается объемный узор, или образовываться повторением узора из пряжи различных цветов, например стилизованные цветы или олени на свитерах.

Примечания

1. ↑ Stewart, Ian. 2001. Pages 48-49.
2. ↑ Stewart, Ian. 2001. Pages 64-65.
3. ↑ Stewart, Ian. 2001. Page 52.
4. ↑ Stewart, Ian. 2001. Pages 82-84.
5. ↑ Stewart, Ian. 2001. Page 60.
6. ↑ Stewart, Ian. 2001. Page 71.
7. ↑ Mandelbrot, Benoît B. The fractal geometry of nature. — Macmillan, 1983.
8. ↑ Falconer, Kenneth. Fractal Geometry: Mathematical Foundations and Applications. — John Wiley, 2003.
9. ↑ Briggs, John. Fractals:The Patterns of Chaos. — Thames and Hudson, 1992. — P. 148.
10. ↑ Batty, Michael (1985-04-04). «Fractals – Geometry Between Dimensions». New Scientist (Holborn Publishing Group) 105 (1450).
11. ↑ Meyer, Yves; Roques, Sylvie. Progress in wavelet analysis and applications: proceedings of the International Conference «Wavelets and Applications,» Toulouse, France – June 1992. — Atlantica Séguier Frontières, 1993. — P. 25.
12. ↑ Carbone, Alessandra; Gromov, Mikhael; Prusinkiewicz, Przemyslaw. Pattern formation in biology, vision and dynamics. — World Scientific, 2000. — P. 78. — ISBN 9789810237929.
13. ↑ Hahn, Horst K.; Georg,Manfred; Peitgen, Heinz-Otto. Fractal aspects of three-dimensional vascular constructive optimization // Fractals in biology and medicine / Losa, Gabriele A.; Nonnenmacher, Theo F.. — Springer, 2005. — P. 55–66.>
14. ↑ Addison, Paul S. Fractals and chaos: an illustrated course. — CRC Press, 1997. — P. 44–46.
15. ↑ Maor, Eli. e: The Story of a Number. Princeton University Press, 2009. Page 135.
16. ↑ Ball, 2009. Shapes pp 29-32.
17. ↑ Kappraff, Jay (2004). «Growth in Plants: A Study in Number». Forma 19: 335–354.
18. ↑ Coxeter, H. S. M. Introduction to geometry. — Wiley, 1961. — P. 169.
19. ↑ Lorenz, Edward N. (March 1963). «Deterministic Nonperiodic Flow». Journal of the Atmospheric Sciences 20 (2): 130–141. DOI:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2. ISSN 1520-0469. Bibcode: 1963JAtS…20..130L. Проверено 3 June 2010.
20. ↑ Ruelle, David. Chance and Chaos. Princeton University Press, 1991.
21. ↑ Lewalle, Jacques. Flow Separation and Secondary Flow: Section 9.1 // Lecture Notes in Incompressible Fluid Dynamics: Phenomenology, Concepts and Analytical Tools. — Syracuse, NY : Syracuse University, 2006..
22. ↑ Информация из справочника интерьерных идей 4living.ru. Архивировано 3 декабря 2012 года.
23. ↑ Ciaccio E. J., Dunn S.M., Akay M. Biosignal pattern recognition and interpretation systems. Part 4 of 4: Review of applications // IEEE Engineering in Medicine and Biology Magazine. — 1994. — Vol. 13, 2006, Issue 2. — P. 269—273.
24. ↑ Гапонова О .В. Электроэнцефалографические паттерны синдрома Веста // Медицинский совет. — 2008.- № 1-2.
25. ↑ Малая меди цинская энциклопедия. — М.: Медицинская энциклопедия. 1991-96 гг.
26. ↑ Небожин А. И., Ситель А. Б. Паттерны боли при биомеханических нарушениях шейного отдела позвоночника // Мануальная терапия. — 2007. — № 1 (25). — С. 2-8.
27. ↑ Паттерны двигательных и чувствительных расстройств при патологии нервных структур в дистальных отделах верхней конечности // Медицинский портал для врачей и студентов doctorspb.ru. 2010. Источник в Интернет: http://doctorspb.ru/articles.php?article_id=1477

wiki2.red

Паттерн — Википедия

плитка — пример использования паттернов в дизайне помещений

Па́ттерн (англ. pattern «образец, шаблон; форма, модель; схема, диаграмма») — схема-образ, действующая как посредствующее представление, или чувственное понятие, благодаря которому в режиме одновременности восприятия и мышления выявляются закономерности, как они существуют в природе и обществе.

Паттерн понимается в этом плане как повторяющийся шаблон или образец. Элементы паттерна повторяются предсказуемо. Так, из графических паттернов складываются красивые узоры.

Каждый из органов восприятия (чувств) воспринимает паттерны в соответствии со своими особенностями.

В науке, в том числе в математике и языкознании, паттерны выявляются путём исследования.

Прямое наблюдение может выявлять визуальные паттерны, как они формируются в природе и в искусстве.
Визуальные паттерны в природе часто хаотичны. Они не копируют друг друга и часто являются фрактальными.

Паттерны в природе включают спирали, меандры, волны, пену, трещины, а также паттерны, созданные благодаря симметрии поворота и отражения. Все подобные паттерны имеют математически описываемую структуру, которая может быть выражена формулами, тем не менее математика сама по себе является поиском регулярностей, и любой конечный продукт применения функций является математическим паттерном.

Когда научные теории исследуют и предсказывают синхронно существующие регулярности в природе и обществе, то это и есть выявление паттернов.
В искусстве и архитектуре для получения определенного устойчивого воздействия декорации и различные визуальные элементы могут комбинироваться и повторяться, образуя паттерны.
В компьютерных науках шаблоны проектирования являются широко используемым решением большого класса проблем программирования.

Под паттерном в медицине понимают устойчивую комбинацию результатов исследований или других признаков (например, симптомов) при сходных жалобах пациента или у больных одной нозологии. Понятие «паттерн» включает несколько признаков (симптомов). Синдром включает один или несколько паттернов. Болезнь включает один или несколько синдромов.

Паттерны в природе

рисунки морских животных Эрнста Геккеля, демонстрирующие различные виды симметрии

Ранние греческие философы, такие как Платон, Пифагор, Эмпедокл, исследовали паттерны, пытаясь объяснить порядок в природе. Современное понимание визуальных паттернов формировалось постепенно с развитием наук.

В XIX веке бельгийский физик Жозеф Плато, изучая мыльные пузыри, сформулировал концепцию минимальной поверхности. Немецкий биолог и художник Эрнст Геккель нарисовал сотни морских организмов, подчёркивая их симметрию. Шотландский биолог Дарси Томпсон первым начал изучение паттернов роста как растений, так и животных, показав, что спиральный рост можно описать простыми уравнениями. В XX веке британский математик Алан Тьюринг предсказал механизмы морфогенеза, которые ответственны за образование пятен и полос. Венгерский биолог Аристид Линденмайер и французско-американский математик Бенуа́ Мандельбро́т показали, как математика фракталов может объяснить паттерны роста растений.

Математика, физика и химия объясняют паттерны в природе на различных уровнях. Паттерны в живых организмах могут быть объяснены биологическими процессами естественного и полового отбора. Изучение формирования паттернов использует компьютерное моделирование для симуляции широкого спектра паттернов.

Виды паттернов в природе

Симметрия

Симметрия для живых организмов является практически всеобщей. У большинства животных наблюдается зеркальная, или билатеральная, симметрия, она также присутствует в листьях растений и некоторых цветах, например орхидеях.^[1] Растения часто имеют круговую, или вращательную, симметрию, как у многих цветов и некоторых животных, например у медуз. Пятилучевая симметрия встречается у иглокожих, таких как морские звёзды, морские ежи и морские лилии^[2].

В неживой природе снежинка имеет красивую шестилучевую симметрию, каждая снежинка уникальна, но один и тот же паттерн повторяется на всех шести её лучах^[3]. Кристаллы обычно имеют разные виды симметрии и габитусы, они могут быть кубическими, шестигранными, восьмигранными, но настоящие кристаллы никогда не имеют пятилучевую симметрию (чего нельзя сказать о квазикристаллах).^[4] Вращательная симметрия встречается в различных явлениях неживой природы, например при всплеске, когда капля падает в водоём,^[5] а также в сферических формах и кольцах планет, таких как Сатурн.^[6]

Деревья, фракталы

самоподобие фрактального листа

Фракталы бесконечно самоподобны.^[7][8][9] Бесконечные повторения в природе невозможны, поэтому ‘фрактальные’ паттерны фрактальны лишь приблизительно. Например, листья папоротников и зонтичных (Apiaceae) самоподобны на 2-м, 3-м или 4-м уровне. Схожие с папоротником паттерны самоподобия встречаются также у животных, включая мшанки, кораллы, гидроидные, а также в неживой природе, преимущественно в электрических разрядах.

Фракталоподобные паттерны широко встречаются в природе, в таких распространённых феноменах, как облака, речные сети, геологические разломы, горы, береговые линии,^[10] окрас животных, снежинки,^[11]кристаллы,^[12] разветвления кровеносных сосудов^[13] и морские волны.^[14]

Спирали

Спирали часто встречаются у растений и некоторых животных, преимущественно моллюсков. Например у наутилусов, головоногих моллюсков, каждая камера его раковины является приблизительной копией предыдущей камеры, увеличенной на определённый коэффициент и представленной в виде логарифмической спирали.^[15] Исходя из современного понимания фракталов, растущая спираль является частным случаем самоподобия.^[16]

Среди растений спирали образуют некоторые виды алоэ, спиралевидным является распределение листьев на стебле, а также других частей у иных растений, например: соцветья астровых, семянные головки подсолнечника или фрукты вроде ананаса^[17]:337 и салака, а также паттерн на шишках, где многочисленные спирали располагаются как по часовой, так и против часовой стрелки.

Спираль произрастания листьев может быть выведена из последовательности чисел Фибоначчи: 1, 1, 2, 3, 5, 8, 13… (каждое следующее число является суммой двух предыдущих). Например, при росте листьев из ствола, один поворот спирали равен двум листьям, поэтому паттерн или соотношение равно 1/2. У орешника соотношение 1/3; у абрикоса 2/5; у груши 3/8; у миндаля оно составляет 5/13.^[18]

Хаос, потоки, меандры

хаос в окраске ракушки Вид на Николаев из космоса. Синусоидальный паттерн, образованный реками — пример меандра

В математике динамическая система является хаотической, если она слишком чувствительна к начальным условиям (так называемый эффект бабочки^[19]).

Теория хаоса считается одним из самых важных факторов, влияющих на возникновение паттернов в природе. Существует связь между хаосом и фракталами — странные аттракторы в хаотических системах имеют фрактальную размерность.^[20]

Турбулентность в газах и жидкостях при преодолении твердого препятствия образует характерные паттерны кручения.

Меандры — это синусообразные изгибы в реках и других каналах, формируемые жидкостью, обычно водой, текущей вдоль изгибов. Если русло не является ровным, размеры и неровность изгибов увеличивается за счёт того, что течение переносит твёрдый материал, обычно песок и гальку к внутренней стороне изгиба. Внешняя часть изгиба остаётся незащищённой, поэтому эрозия усиливается, увеличивая темпы меандрирования.^[21]

Волны, дюны

Под влиянием ветра на поверхности воды и песка в природе образовываются схожие по строению хаотические паттерны, оставляющие рябь, называемые волнами на воде и дюнами на песке. Под действием ветра происходит неравномерное распределение, возвышенные участки чередуются с понижениями уровня.

Частным случаем дюн являются барханы.

Пузыри, пена

Мыльные пузыри образуют пену

Замощение

Замощение — разбиение без каких-либо накладок и без пробелов. Наиболее известным примером замощения в природе являются пчелиные соты, где шестиугольный паттерн многократно дублируется, заполняя всё пространство улья.

Трещины

Пятна и полосы

Паттерны в архитектуре

Паттерны в дизайне

Паттерны (повторяющиеся элементы) широко используются для украшения среды обитания человека — от лепнины, тротуарной плитки, обоев, паркета и кафеля до орнаментов в одежде, раскраски тканей и использования узоров в оформлении всевозможной печатной продукции. Наиболее популярные паттерны имеют имена, Клетка, Гусиные лапки, Бута, Турецкие огурцы, Алагрек, Меандр.

Паттерны часто употребляются в исламском мире. Искусствоведы подразделяют исламские узоры на стилизованные растительные, которые называются Арабеска, и геометрические, называемые Мореска.^[22]

Паттерны для детей

Простым инструментом для создания паттернов является спирограф.

Наблюдать причудливые паттерны можно с помощью калейдоскопа.

Паттерны в медицине

В медицине термин «паттерн» употребляют при анализе, например, кардиограмм, энцефалограмм и результатов других исследований, понимая под ним^[23] одинаковую последовательность колебаний биопотенциалов, повторяющуюся в одном или нескольких отведениях при одинаковых состояниях и условиях^[24]

Термин паттерн используется для обозначения последовательности нервных импульсов, имеющей определённое информационное значение^[25], например, «паттерны боли при биомеханических нарушениях суставов краниовертебрального перехода и шейного отдела позвоночника»^[26] или «паттерны двигательных и чувствительных расстройств при патологии нервных структур в дистальных отделах верхней конечности»^[27].

Паттерны широко представлены в глоссарии мануальных терапевтов (например паттерн ходьбы), рефлексотерапевтов (например, паттерн сырости-жара) и прикладных кинезиологов (например, паттерн дыхания).

Паттерны вязания

В вязании часто используются схемы рисунков, которые повторяются через определенное количество столбцов и рядов. Один такой рисунок, предназначенный для многократного повторения в вязаном изделии, и называется паттерном. Паттерн может состоять из различных видов петель, в результате получается объемный узор, или образовываться повторением узора из пряжи различных цветов, например стилизованные цветы или олени на свитерах.

Примечания

1. ↑ Stewart, Ian. 2001. Pages 48-49.
2. ↑ Stewart, Ian. 2001. Pages 64-65.
3. ↑ Stewart, Ian. 2001. Page 52.
4. ↑ Stewart, Ian. 2001. Pages 82-84.
5. ↑ Stewart, Ian. 2001. Page 60.
6. ↑ Stewart, Ian. 2001. Page 71.
7. ↑ Mandelbrot, Benoît B. The fractal geometry of nature. — Macmillan, 1983.
8. ↑ Falconer, Kenneth. Fractal Geometry: Mathematical Foundations and Applications. — John Wiley, 2003.
9. ↑ Briggs, John. Fractals:The Patterns of Chaos. — Thames and Hudson, 1992. — P. 148.
10. ↑ Batty, Michael (1985-04-04). «Fractals – Geometry Between Dimensions». New Scientist (Holborn Publishing Group) 105 (1450).
11. ↑ Meyer, Yves; Roques, Sylvie. Progress in wavelet analysis and applications: proceedings of the International Conference «Wavelets and Applications,» Toulouse, France – June 1992. — Atlantica Séguier Frontières, 1993. — P. 25.
12. ↑ Carbone, Alessandra; Gromov, Mikhael; Prusinkiewicz, Przemyslaw. Pattern formation in biology, vision and dynamics. — World Scientific, 2000. — P. 78. — ISBN 9789810237929.
13. ↑ Hahn, Horst K.; Georg,Manfred; Peitgen, Heinz-Otto. Fractal aspects of three-dimensional vascular constructive optimization // Fractals in biology and medicine / Losa, Gabriele A.; Nonnenmacher, Theo F.. — Springer, 2005. — P. 55–66.>
14. ↑ Addison, Paul S. Fractals and chaos: an illustrated course. — CRC Press, 1997. — P. 44–46.
15. ↑ Maor, Eli. e: The Story of a Number. Princeton University Press, 2009. Page 135.
16. ↑ Ball, 2009. Shapes pp 29-32.
17. ↑ Kappraff, Jay (2004). «Growth in Plants: A Study in Number». Forma 19: 335–354.
18. ↑ Coxeter, H. S. M. Introduction to geometry. — Wiley, 1961. — P. 169.
19. ↑ Lorenz, Edward N. (March 1963). «Deterministic Nonperiodic Flow». Journal of the Atmospheric Sciences 20 (2): 130–141. DOI:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2. ISSN 1520-0469. Bibcode: 1963JAtS…20..130L. Проверено 3 June 2010.
20. ↑ Ruelle, David. Chance and Chaos. Princeton University Press, 1991.
21. ↑ Lewalle, Jacques. Flow Separation and Secondary Flow: Section 9.1 // Lecture Notes in Incompressible Fluid Dynamics: Phenomenology, Concepts and Analytical Tools. — Syracuse, NY : Syracuse University, 2006..
22. ↑ Информация из справочника интерьерных идей 4living.ru. Архивировано 3 декабря 2012 года.
23. ↑ Ciaccio E. J., Dunn S.M., Akay M. Biosignal pattern recognition and interpretation systems. Part 4 of 4: Review of applications // IEEE Engineering in Medicine and Biology Magazine. — 1994. — Vol. 13, 2006, Issue 2. — P. 269—273.
24. ↑ Гапонова О .В. Электроэнцефалографические паттерны синдрома Веста // Медицинский совет. — 2008.- № 1-2.
25. ↑ Малая меди цинская энциклопедия. — М.: Медицинская энциклопедия. 1991-96 гг.
26. ↑ Небожин А. И., Ситель А. Б. Паттерны боли при биомеханических нарушениях шейного отдела позвоночника // Мануальная терапия. — 2007. — № 1 (25). — С. 2-8.
27. ↑ Паттерны двигательных и чувствительных расстройств при патологии нервных структур в дистальных отделах верхней конечности // Медицинский портал для врачей и студентов doctorspb.ru. 2010. Источник в Интернет: http://doctorspb.ru/articles.php?article_id=1477

wikipedia.green

📌 Паттерн (психология) — это… 🎓 Что такое Паттерн (психология)?

Cтереотип (греч. stereos + typos — «твердый» + «отпечаток») . Изначально «стереотип» — метафора относительно мышления, пришедшая из типографского дела, где стереотип — монолитная печатная форма, копия с типографского набора или клише, используемая для ротационной печати многотиражных изданий. В современной социальной теории и психологии существуют различные определения понятия «Стереотип», в зависимости от методологического направления научной школы.

Стереотип — это устоявшееся отношение к происходящим событиям, выработанное на основе сравнения их с внутренними идеалами. Система стереотипов составляет — миропонимание.

Понятие «стереотип» в общественно-политический западный дискурс вошло с лёгкой руки Уолтера Липпмана, которое он применил в описании своей оригинальной концепции общественного мнения в 1922 г.

Согласно Липпману [1], возможно вывести следующее определение: стереотип — это принятый в исторической общности образец восприятия, фильтрации, интерпретации информации при распознавании и узнавании окружающего мира, основанный на предшествующем социальном опыте . Система стереотипов представляет собой социальную реальность.

Определение Уолтера Липпмана обладает значительным познавательным потенциалом для социологов и социальных психологов, т.к. позволяет проводить различение между тем, что предстаёт и, что представляют. Так, в 1999 году на конгрессе Европейской ассоциации экспериментальной социальной психологии, проходившем в Оксфорде, из 33 симпозиумов 13 были сфокусированы на проблематике стереотипов, предубеждений и дискриминации. В своей книге “Общественное мнение” Липпман предвосхитил основные смыслы, которые в дальнейшем исследователи обнаружили в стереотипах, а само понятие прочно вошло в обыденный язык [3]

Экономия усилий

Область построения стереотипов простирается от бредовых фантазий до осознанного использования учёными округлённых результатов вычислений. Вся человеческая культура — это, главным образом (в интерпретации Липпмана, разумеется) отбор, реорганизация, отслеживание разных моделей среды. Т.е. формирование стереотипов это экономия собственных усилий, т.к. попытка увидеть все вещи заново и в подробностях, а не как типы и обобщения, утомительна, а для занятого человека практически обречена на провал. Дополнительно следует отметить случаи отказа от типизаций: в близком кругу нет способа подменить чем-либо индивидуализированное понимание или как-то сэкономить на нем. Те, кого мы любим и кем восхищаемся, в большинстве своем – это мужчины и женщины, знают скорее нас самих, а не классификацию, под которую нас можно подвести.

Разметка мира

Помимо экономии усилий, стереотипы, видимо, выполняют и ещё одну функцию: системы стереотипов могут служить ядром нашей личной традиции, способом защиты нашего положения в обществе. Они представляют собой упорядоченную, более или менее непротиворечивую картину мира. В ней удобно разместились наши привычки, вкусы, способности, удовольствия и надежды. Стереотипная картина мира может быть не полной, но это картина возможного мира, к которому мы приспособились. В этом мире люди и предметы занимают предназначенные им места и действуют ожидаемым образом. Мы чувствуем себя в этом мире как дома, мы составная часть его. Поэтому неудивительно, что любое изменение стереотипов воспринимается как атака на основы мироздания. Это атака на основания нашего мира, и когда речь идет о серьезных вещах, то нам на самом деле не так просто допустить, что существует какое-то различие между нашим личным миром и миром вообще. Система стереотипов не просто способ замены пышного разнообразия и беспорядочной реальности на упорядоченное представление о ней, только сокращенный и упрощенный путь восприятия. Стереотипы служат гарантией нашего самоуважения; проецируют во внешний мир осознание наших ценностей; защищают наше положение в обществе и наши права, А следовательно, стереотипы наполнены чувствами, предпочтениями, приязнью или неприязнью, ассоциируются со страхами, желаниями, влечениями, гордостью, надеждой. Объект, который активизирует стереотип, оценивается в связи с соответствующими эмоциями.

Стереотипы и предрассудки

В повседневной жизни именно предшествующее получению соответствующих данных суждение содержит в себе вывод, который эти данные чаще всего и подтверждают. Cправедливость, прощение, истина не входят в это суждение, ибо оно предшествует получению фактических данных. Предрассудок, конечно, может быть выявлен, учтен и доработан. Но так как срок жизни человека ограничен, тот должен за отпущенное ему время получить все сведения, необходимые для освоения обширной цивилизации, поэтому ему не обойтись без предрассудков. Качество его мышления и деятельности будет зависеть от того, являются ли эти предрассудки доброжелательными по отношению к другим людям и идеям, возбуждают ли они скорее любовь по отношению к тому, что явно воспринимается как благо, или ненависть по отношению к тому, что не входит в их представление о благе.

Динамика стереотипов

Стереотип начинает действовать еще до того, как включается разум. Это накладывает специфический отпечаток на данные, которые воспринимаются нашими органами чувств еще до того, как эти данные достигают рассудка. Ничто так не сопротивляется образованию или критике, как стереотип, так как Он накладывает свой отпечаток на фактические данные в момент их восприятия.

В определенной степени внешние стимулы, особенно сказанные или напечатанные, активизируют некоторую часть системы стереотипов, так что непосредственное впечатление и ранее сложившееся мнение появляются в сознании одновременно.

В случаях когда опыт вступает в противоречие со стереотипом, возможен двоякий исход: если индивид уже утратил определенную гибкость или ему в силу какой-то значительной заинтересованности крайне неудобно менять свои стереотипы, он может проигнорировать это противоречие и счесть его исключением, подтверждающим правило, или найти какую-то ошибку, а затем забыть об этом событии. Но если он не утратил любопытства или способности думать, то новшество интегрируется в уже существующую картину мира и изменяет ее.

Гендерные стереотипы

Гендерные стереотипы — сформировавшиеся в культуре обобщенные представления (убеждения) о том, как в действительности ведут себя или должны вести себя мужчины и женщины. В основном, с мужчиной ассоциируются такие слова как сильный, жестокий, равнодушный, драчливый и самоуверенный. В семье мужчина — хозяин, лидер, защитник. Женщина характеризуется как скромная, вежливая, следящая за своей внешностью. В семье она — воспитательница и кухарка.

Отечественная традиция

В 20–30е годы ХХ столетия физиологическая школа И. П. Павлова активно занималась изучением феномена, названного Павловым “динамической стереотипией”. В основу представления русской физиологической школы о стереотипе легла способность мозга фиксировать однотипные изменения среды и соответственно реагировать на эти изменения.

Определение динамического стереотипа (по И.П. Павлову ) —слаженная уравновешенная система внутренних процессов больших полушарий, соответствующая внешней системе условных раздражителей. Отметим, что определение академика Павлова содержательно соответсвует определению системности Э. А. Асратяна. Возможно привести и другое определение, где стереотип это цепь нервных следов от прежних раздражителей, срабатывающих, в отличие от условных и безусловных рефлексов, в отсутствие внешнего стимула [2]

Осознание необходимости концептуализации стереотипа пришло в ходе экспериментов по выработке условных рефлексов на чередующиеся через одинаковые паузы положительные и отрицательные звуковые и кожные раздражители. Выявленный эффект заключался в том, что после укрепления такой деятельности новые рефлексы вырабатывались очень быстро, а в ряде случаев возникали с первого же применения новых раздражителей, при этом воспроизводился ранее сформированный ритм возбуждения и торможения, соответствующий порядку применения положительных и отрицательных сигналов.

На изменение внешнего стереотипа мозг реагирует рядом характерных перестроек, которые отражаются в отдельных звеньях системы, во всей системе или, наконец, всей высшей нервной деятельности. Внешние изменения могут привести как к улучшению, так и к ухудшению протекания высших функций вплоть до развития глубокого невроза. Павлов обратил внимание, что «процессы установки стереотипа и нарушений его и есть субъективно разнообразные положительные и отрицательные чувства».

Содержательно связь между “динамической стереотипией” Павлова и стереотипами Липпмана представляется достаточно прозрачной (для обоих важно что стереотип это слепок окружающей реальности, позволяющий адаптироваться к многообразию), хотя различие подходов к изучению понятно: Липпману акцентирует внимание на социальности стереотипов и того, какое значение они играют в функционировании общества и общностей, а Павлов на физиологии нервной деятельности.

См. также

Источники

1. Липпман У. Общественное мнение /пер. с англ. Т. В. Барчунова, под ред. К. А. Левинсон, К. В. Петренко. М.: Институт Фонда «Общественное мнение», 2004
2. Судаков К.В. Динамические стереотипы, или Информационные отпечатки действительности. М.: ПЕР СЭ, 2002
3. Ослон А. Уолтер Липпман о стереотипах: выписки из книги “Общественное мнение” // Социальная реальность, 2006, №4, C. 125 — 141.

Wikimedia Foundation. 2010.

dic.academic.ru

Паттерн — Википедия. Что такое Паттерн

плитка — пример использования паттернов в дизайне помещений

Па́ттерн (англ. pattern «образец, шаблон; форма, модель; схема, диаграмма») — схема-образ, действующая как посредствующее представление, или чувственное понятие, благодаря которому в режиме одновременности восприятия и мышления выявляются закономерности, как они существуют в природе и обществе.

Паттерн понимается в этом плане как повторяющийся шаблон или образец. Элементы паттерна повторяются предсказуемо. Так, из графических паттернов складываются красивые узоры.

Каждый из органов восприятия (чувств) воспринимает паттерны в соответствии со своими особенностями.

В науке, в том числе в математике и языкознании, паттерны выявляются путём исследования.

Прямое наблюдение может выявлять визуальные паттерны, как они формируются в природе и в искусстве.
Визуальные паттерны в природе часто хаотичны. Они не копируют друг друга и часто являются фрактальными.

Паттерны в природе включают спирали, меандры, волны, пену, трещины, а также паттерны, созданные благодаря симметрии поворота и отражения. Все подобные паттерны имеют математически описываемую структуру, которая может быть выражена формулами, тем не менее математика сама по себе является поиском регулярностей, и любой конечный продукт применения функций является математическим паттерном.

Когда научные теории исследуют и предсказывают синхронно существующие регулярности в природе и обществе, то это и есть выявление паттернов.
В искусстве и архитектуре для получения определенного устойчивого воздействия декорации и различные визуальные элементы могут комбинироваться и повторяться, образуя паттерны.
В компьютерных науках шаблоны проектирования являются широко используемым решением большого класса проблем программирования.

Под паттерном в медицине понимают устойчивую комбинацию результатов исследований или других признаков (например, симптомов) при сходных жалобах пациента или у больных одной нозологии. Понятие «паттерн» включает несколько признаков (симптомов). Синдром включает один или несколько паттернов. Болезнь включает один или несколько синдромов.

Паттерны в природе

рисунки морских животных Эрнста Геккеля, демонстрирующие различные виды симметрии

Ранние греческие философы, такие как Платон, Пифагор, Эмпедокл, исследовали паттерны, пытаясь объяснить порядок в природе. Современное понимание визуальных паттернов формировалось постепенно с развитием наук.

В XIX веке бельгийский физик Жозеф Плато, изучая мыльные пузыри, сформулировал концепцию минимальной поверхности. Немецкий биолог и художник Эрнст Геккель нарисовал сотни морских организмов, подчёркивая их симметрию. Шотландский биолог Дарси Томпсон первым начал изучение паттернов роста как растений, так и животных, показав, что спиральный рост можно описать простыми уравнениями. В XX веке британский математик Алан Тьюринг предсказал механизмы морфогенеза, которые ответственны за образование пятен и полос. Венгерский биолог Аристид Линденмайер и французско-американский математик Бенуа́ Мандельбро́т показали, как математика фракталов может объяснить паттерны роста растений.

Математика, физика и химия объясняют паттерны в природе на различных уровнях. Паттерны в живых организмах могут быть объяснены биологическими процессами естественного и полового отбора. Изучение формирования паттернов использует компьютерное моделирование для симуляции широкого спектра паттернов.

Виды паттернов в природе

Симметрия

Симметрия для живых организмов является практически всеобщей. У большинства животных наблюдается зеркальная, или билатеральная, симметрия, она также присутствует в листьях растений и некоторых цветах, например орхидеях.^[1] Растения часто имеют круговую, или вращательную, симметрию, как у многих цветов и некоторых животных, например у медуз. Пятилучевая симметрия встречается у иглокожих, таких как морские звёзды, морские ежи и морские лилии^[2].

В неживой природе снежинка имеет красивую шестилучевую симметрию, каждая снежинка уникальна, но один и тот же паттерн повторяется на всех шести её лучах^[3]. Кристаллы обычно имеют разные виды симметрии и габитусы, они могут быть кубическими, шестигранными, восьмигранными, но настоящие кристаллы никогда не имеют пятилучевую симметрию (чего нельзя сказать о квазикристаллах).^[4] Вращательная симметрия встречается в различных явлениях неживой природы, например при всплеске, когда капля падает в водоём,^[5] а также в сферических формах и кольцах планет, таких как Сатурн.^[6]

Деревья, фракталы

самоподобие фрактального листа

Фракталы бесконечно самоподобны.^[7][8][9] Бесконечные повторения в природе невозможны, поэтому ‘фрактальные’ паттерны фрактальны лишь приблизительно. Например, листья папоротников и зонтичных (Apiaceae) самоподобны на 2-м, 3-м или 4-м уровне. Схожие с папоротником паттерны самоподобия встречаются также у животных, включая мшанки, кораллы, гидроидные, а также в неживой природе, преимущественно в электрических разрядах.

Фракталоподобные паттерны широко встречаются в природе, в таких распространённых феноменах, как облака, речные сети, геологические разломы, горы, береговые линии,^[10] окрас животных, снежинки,^[11]кристаллы,^[12] разветвления кровеносных сосудов^[13] и морские волны.^[14]

Спирали

Спирали часто встречаются у растений и некоторых животных, преимущественно моллюсков. Например у наутилусов, головоногих моллюсков, каждая камера его раковины является приблизительной копией предыдущей камеры, увеличенной на определённый коэффициент и представленной в виде логарифмической спирали.^[15] Исходя из современного понимания фракталов, растущая спираль является частным случаем самоподобия.^[16]

Среди растений спирали образуют некоторые виды алоэ, спиралевидным является распределение листьев на стебле, а также других частей у иных растений, например: соцветья астровых, семянные головки подсолнечника или фрукты вроде ананаса^[17]:337 и салака, а также паттерн на шишках, где многочисленные спирали располагаются как по часовой, так и против часовой стрелки.

Спираль произрастания листьев может быть выведена из последовательности чисел Фибоначчи: 1, 1, 2, 3, 5, 8, 13… (каждое следующее число является суммой двух предыдущих). Например, при росте листьев из ствола, один поворот спирали равен двум листьям, поэтому паттерн или соотношение равно 1/2. У орешника соотношение 1/3; у абрикоса 2/5; у груши 3/8; у миндаля оно составляет 5/13.^[18]

Хаос, потоки, меандры

хаос в окраске ракушки Вид на Николаев из космоса. Синусоидальный паттерн, образованный реками — пример меандра

В математике динамическая система является хаотической, если она слишком чувствительна к начальным условиям (так называемый эффект бабочки^[19]).

Теория хаоса считается одним из самых важных факторов, влияющих на возникновение паттернов в природе. Существует связь между хаосом и фракталами — странные аттракторы в хаотических системах имеют фрактальную размерность.^[20]

Турбулентность в газах и жидкостях при преодолении твердого препятствия образует характерные паттерны кручения.

Меандры — это синусообразные изгибы в реках и других каналах, формируемые жидкостью, обычно водой, текущей вдоль изгибов. Если русло не является ровным, размеры и неровность изгибов увеличивается за счёт того, что течение переносит твёрдый материал, обычно песок и гальку к внутренней стороне изгиба. Внешняя часть изгиба остаётся незащищённой, поэтому эрозия усиливается, увеличивая темпы меандрирования.^[21]

Волны, дюны

Под влиянием ветра на поверхности воды и песка в природе образовываются схожие по строению хаотические паттерны, оставляющие рябь, называемые волнами на воде и дюнами на песке. Под действием ветра происходит неравномерное распределение, возвышенные участки чередуются с понижениями уровня.

Частным случаем дюн являются барханы.

Пузыри, пена

Мыльные пузыри образуют пену

Замощение

Замощение — разбиение без каких-либо накладок и без пробелов. Наиболее известным примером замощения в природе являются пчелиные соты, где шестиугольный паттерн многократно дублируется, заполняя всё пространство улья.

Трещины

Пятна и полосы

Паттерны в архитектуре

Паттерны в дизайне

Паттерны (повторяющиеся элементы) широко используются для украшения среды обитания человека — от лепнины, тротуарной плитки, обоев, паркета и кафеля до орнаментов в одежде, раскраски тканей и использования узоров в оформлении всевозможной печатной продукции. Наиболее популярные паттерны имеют имена, Клетка, Гусиные лапки, Бута, Турецкие огурцы, Алагрек, Меандр.

Паттерны часто употребляются в исламском мире. Искусствоведы подразделяют исламские узоры на стилизованные растительные, которые называются Арабеска, и геометрические, называемые Мореска.^[22]

Паттерны для детей

Простым инструментом для создания паттернов является спирограф.

Наблюдать причудливые паттерны можно с помощью калейдоскопа.

Паттерны в медицине

В медицине термин «паттерн» употребляют при анализе, например, кардиограмм, энцефалограмм и результатов других исследований, понимая под ним^[23] одинаковую последовательность колебаний биопотенциалов, повторяющуюся в одном или нескольких отведениях при одинаковых состояниях и условиях^[24]

Термин паттерн используется для обозначения последовательности нервных импульсов, имеющей определённое информационное значение^[25], например, «паттерны боли при биомеханических нарушениях суставов краниовертебрального перехода и шейного отдела позвоночника»^[26] или «паттерны двигательных и чувствительных расстройств при патологии нервных структур в дистальных отделах верхней конечности»^[27].

Паттерны широко представлены в глоссарии мануальных терапевтов (например паттерн ходьбы), рефлексотерапевтов (например, паттерн сырости-жара) и прикладных кинезиологов (например, паттерн дыхания).

Паттерны вязания

В вязании часто используются схемы рисунков, которые повторяются через определенное количество столбцов и рядов. Один такой рисунок, предназначенный для многократного повторения в вязаном изделии, и называется паттерном. Паттерн может состоять из различных видов петель, в результате получается объемный узор, или образовываться повторением узора из пряжи различных цветов, например стилизованные цветы или олени на свитерах.

Примечания

1. ↑ Stewart, Ian. 2001. Pages 48-49.
2. ↑ Stewart, Ian. 2001. Pages 64-65.
3. ↑ Stewart, Ian. 2001. Page 52.
4. ↑ Stewart, Ian. 2001. Pages 82-84.
5. ↑ Stewart, Ian. 2001. Page 60.
6. ↑ Stewart, Ian. 2001. Page 71.
7. ↑ Mandelbrot, Benoît B. The fractal geometry of nature. — Macmillan, 1983.
8. ↑ Falconer, Kenneth. Fractal Geometry: Mathematical Foundations and Applications. — John Wiley, 2003.
9. ↑ Briggs, John. Fractals:The Patterns of Chaos. — Thames and Hudson, 1992. — P. 148.
10. ↑ Batty, Michael (1985-04-04). «Fractals – Geometry Between Dimensions». New Scientist (Holborn Publishing Group) 105 (1450).
11. ↑ Meyer, Yves; Roques, Sylvie. Progress in wavelet analysis and applications: proceedings of the International Conference «Wavelets and Applications,» Toulouse, France – June 1992. — Atlantica Séguier Frontières, 1993. — P. 25.
12. ↑ Carbone, Alessandra; Gromov, Mikhael; Prusinkiewicz, Przemyslaw. Pattern formation in biology, vision and dynamics. — World Scientific, 2000. — P. 78. — ISBN 9789810237929.
13. ↑ Hahn, Horst K.; Georg,Manfred; Peitgen, Heinz-Otto. Fractal aspects of three-dimensional vascular constructive optimization // Fractals in biology and medicine / Losa, Gabriele A.; Nonnenmacher, Theo F.. — Springer, 2005. — P. 55–66.>
14. ↑ Addison, Paul S. Fractals and chaos: an illustrated course. — CRC Press, 1997. — P. 44–46.
15. ↑ Maor, Eli. e: The Story of a Number. Princeton University Press, 2009. Page 135.
16. ↑ Ball, 2009. Shapes pp 29-32.
17. ↑ Kappraff, Jay (2004). «Growth in Plants: A Study in Number». Forma 19: 335–354.
18. ↑ Coxeter, H. S. M. Introduction to geometry. — Wiley, 1961. — P. 169.
19. ↑ Lorenz, Edward N. (March 1963). «Deterministic Nonperiodic Flow». Journal of the Atmospheric Sciences 20 (2): 130–141. DOI:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2. ISSN 1520-0469. Bibcode: 1963JAtS…20..130L. Проверено 3 June 2010.
20. ↑ Ruelle, David. Chance and Chaos. Princeton University Press, 1991.
21. ↑ Lewalle, Jacques. Flow Separation and Secondary Flow: Section 9.1 // Lecture Notes in Incompressible Fluid Dynamics: Phenomenology, Concepts and Analytical Tools. — Syracuse, NY : Syracuse University, 2006..
22. ↑ Информация из справочника интерьерных идей 4living.ru (недоступная ссылка — история). Проверено 4 апреля 2013. Архивировано 3 декабря 2012 года.
23. ↑ Ciaccio E. J., Dunn S.M., Akay M. Biosignal pattern recognition and interpretation systems. Part 4 of 4: Review of applications // IEEE Engineering in Medicine and Biology Magazine. — 1994. — Vol. 13, 2006, Issue 2. — P. 269—273.
24. ↑ Гапонова О .В. Электроэнцефалографические паттерны синдрома Веста // Медицинский совет. — 2008.- № 1-2.
25. ↑ Малая меди цинская энциклопедия. — М.: Медицинская энциклопедия. 1991-96 гг.
26. ↑ Небожин А. И., Ситель А. Б. Паттерны боли при биомеханических нарушениях шейного отдела позвоночника // Мануальная терапия. — 2007. — № 1 (25). — С. 2-8.
27. ↑ Паттерны двигательных и чувствительных расстройств при патологии нервных структур в дистальных отделах верхней конечности // Медицинский портал для врачей и студентов doctorspb.ru. 2010. Источник в Интернет: http://doctorspb.ru/articles.php?article_id=1477

wiki.sc

Паттерн — WiKi

плитка — пример использования паттернов в дизайне помещений

Па́ттерн (англ. pattern «образец, шаблон; форма, модель; схема, диаграмма») — схема-образ, действующая как посредствующее представление, или чувственное понятие, благодаря которому в режиме одновременности восприятия и мышления выявляются закономерности, как они существуют в природе и обществе.

Паттерн понимается в этом плане как повторяющийся шаблон или образец. Элементы паттерна повторяются предсказуемо. Так, из графических паттернов складываются красивые узоры.

Каждый из органов восприятия (чувств) воспринимает паттерны в соответствии со своими особенностями.

В науке, в том числе в математике и языкознании, паттерны выявляются путём исследования.

Прямое наблюдение может выявлять визуальные паттерны, как они формируются в природе и в искусстве.
Визуальные паттерны в природе часто хаотичны. Они не копируют друг друга и часто являются фрактальными.

Паттерны в природе включают спирали, меандры, волны, пену, трещины, а также паттерны, созданные благодаря симметрии поворота и отражения. Все подобные паттерны имеют математически описываемую структуру, которая может быть выражена формулами, тем не менее математика сама по себе является поиском регулярностей, и любой конечный продукт применения функций является математическим паттерном.

Когда научные теории исследуют и предсказывают синхронно существующие регулярности в природе и обществе, то это и есть выявление паттернов.
В искусстве и архитектуре для получения определенного устойчивого воздействия декорации и различные визуальные элементы могут комбинироваться и повторяться, образуя паттерны.
В компьютерных науках шаблоны проектирования являются широко используемым решением большого класса проблем программирования.

Под паттерном в медицине понимают устойчивую комбинацию результатов исследований или других признаков (например, симптомов) при сходных жалобах пациента или у больных одной нозологии. Понятие «паттерн» включает несколько признаков (симптомов). Синдром включает один или несколько паттернов. Болезнь включает один или несколько синдромов.

Паттерны в природе

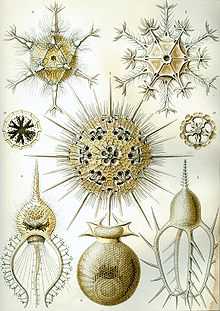  рисунки морских животных Эрнста Геккеля, демонстрирующие различные виды симметрии

Ранние греческие философы, такие как Платон, Пифагор, Эмпедокл, исследовали паттерны, пытаясь объяснить порядок в природе. Современное понимание визуальных паттернов формировалось постепенно с развитием наук.

В XIX веке бельгийский физик Жозеф Плато, изучая мыльные пузыри, сформулировал концепцию минимальной поверхности. Немецкий биолог и художник Эрнст Геккель нарисовал сотни морских организмов, подчёркивая их симметрию. Шотландский биолог Дарси Томпсон первым начал изучение паттернов роста как растений, так и животных, показав, что спиральный рост можно описать простыми уравнениями. В XX веке британский математик Алан Тьюринг предсказал механизмы морфогенеза, которые ответственны за образование пятен и полос. Венгерский биолог Аристид Линденмайер и французско-американский математик Бенуа́ Мандельбро́т показали, как математика фракталов может объяснить паттерны роста растений.

Математика, физика и химия объясняют паттерны в природе на различных уровнях. Паттерны в живых организмах могут быть объяснены биологическими процессами естественного и полового отбора. Изучение формирования паттернов использует компьютерное моделирование для симуляции широкого спектра паттернов.

Виды паттернов в природе

Симметрия

Симметрия для живых организмов является практически всеобщей. У большинства животных наблюдается зеркальная, или билатеральная, симметрия, она также присутствует в листьях растений и некоторых цветах, например орхидеях.^[1] Растения часто имеют круговую, или вращательную, симметрию, как у многих цветов и некоторых животных, например у медуз. Пятилучевая симметрия встречается у иглокожих, таких как морские звёзды, морские ежи и морские лилии^[2].

В неживой природе снежинка имеет красивую шестилучевую симметрию, каждая снежинка уникальна, но один и тот же паттерн повторяется на всех шести её лучах^[3]. Кристаллы обычно имеют разные виды симметрии и габитусы, они могут быть кубическими, шестигранными, восьмигранными, но настоящие кристаллы никогда не имеют пятилучевую симметрию (чего нельзя сказать о квазикристаллах).^[4] Вращательная симметрия встречается в различных явлениях неживой природы, например при всплеске, когда капля падает в водоём,^[5] а также в сферических формах и кольцах планет, таких как Сатурн.^[6]

Деревья, фракталы

  самоподобие фрактального листа

Фракталы бесконечно самоподобны.^[7][8][9] Бесконечные повторения в природе невозможны, поэтому ‘фрактальные’ паттерны фрактальны лишь приблизительно. Например, листья папоротников и зонтичных (Apiaceae) самоподобны на 2-м, 3-м или 4-м уровне. Схожие с папоротником паттерны самоподобия встречаются также у животных, включая мшанки, кораллы, гидроидные, а также в неживой природе, преимущественно в электрических разрядах.

Фракталоподобные паттерны широко встречаются в природе, в таких распространённых феноменах, как облака, речные сети, геологические разломы, горы, береговые линии,^[10] окрас животных, снежинки,^[11]кристаллы,^[12] разветвления кровеносных сосудов^[13] и морские волны.^[14]

Спирали

Спирали часто встречаются у растений и некоторых животных, преимущественно моллюсков. Например у наутилусов, головоногих моллюсков, каждая камера его раковины является приблизительной копией предыдущей камеры, увеличенной на определённый коэффициент и представленной в виде логарифмической спирали.^[15] Исходя из современного понимания фракталов, растущая спираль является частным случаем самоподобия.^[16]

Среди растений спирали образуют некоторые виды алоэ, спиралевидным является распределение листьев на стебле, а также других частей у иных растений, например: соцветья астровых, семянные головки подсолнечника или фрукты вроде ананаса^[17]:337 и салака, а также паттерн на шишках, где многочисленные спирали располагаются как по часовой, так и против часовой стрелки.

Спираль произрастания листьев может быть выведена из последовательности чисел Фибоначчи: 1, 1, 2, 3, 5, 8, 13… (каждое следующее число является суммой двух предыдущих). Например, при росте листьев из ствола, один поворот спирали равен двум листьям, поэтому паттерн или соотношение равно 1/2. У орешника соотношение 1/3; у абрикоса 2/5; у груши 3/8; у миндаля оно составляет 5/13.^[18]

Хаос, потоки, меандры

  хаос в окраске ракушки   Вид на Николаев из космоса. Синусоидальный паттерн, образованный реками — пример меандра

В математике динамическая система является хаотической, если она слишком чувствительна к начальным условиям (так называемый эффект бабочки^[19]).

Теория хаоса считается одним из самых важных факторов, влияющих на возникновение паттернов в природе. Существует связь между хаосом и фракталами — странные аттракторы в хаотических системах имеют фрактальную размерность.^[20]

Турбулентность в газах и жидкостях при преодолении твердого препятствия образует характерные паттерны кручения.

Меандры — это синусообразные изгибы в реках и других каналах, формируемые жидкостью, обычно водой, текущей вдоль изгибов. Если русло не является ровным, размеры и неровность изгибов увеличивается за счёт того, что течение переносит твёрдый материал, обычно песок и гальку к внутренней стороне изгиба. Внешняя часть изгиба остаётся незащищённой, поэтому эрозия усиливается, увеличивая темпы меандрирования.^[21]

Волны, дюны

Под влиянием ветра на поверхности воды и песка в природе образовываются схожие по строению хаотические паттерны, оставляющие рябь, называемые волнами на воде и дюнами на песке. Под действием ветра происходит неравномерное распределение, возвышенные участки чередуются с понижениями уровня.

Частным случаем дюн являются барханы.

Пузыри, пена

  Мыльные пузыри образуют пену

Замощение

Замощение — разбиение без каких-либо накладок и без пробелов. Наиболее известным примером замощения в природе являются пчелиные соты, где шестиугольный паттерн многократно дублируется, заполняя всё пространство улья.

Трещины

Пятна и полосы

Паттерны в архитектуре

Паттерны в дизайне

Паттерны (повторяющиеся элементы) широко используются для украшения среды обитания человека — от лепнины, тротуарной плитки, обоев, паркета и кафеля до орнаментов в одежде, раскраски тканей и использования узоров в оформлении всевозможной печатной продукции. Наиболее популярные паттерны имеют имена, Клетка, Гусиные лапки, Бута, Турецкие огурцы, Алагрек, Меандр.

Паттерны часто употребляются в исламском мире. Искусствоведы подразделяют исламские узоры на стилизованные растительные, которые называются Арабеска, и геометрические, называемые Мореска.^[22]

Паттерны для детей

Простым инструментом для создания паттернов является спирограф.

Наблюдать причудливые паттерны можно с помощью калейдоскопа.

Паттерны в медицине

В медицине термин «паттерн» употребляют при анализе, например, кардиограмм, энцефалограмм и результатов других исследований, понимая под ним^[23] одинаковую последовательность колебаний биопотенциалов, повторяющуюся в одном или нескольких отведениях при одинаковых состояниях и условиях^[24]

Термин паттерн используется для обозначения последовательности нервных импульсов, имеющей определённое информационное значение^[25], например, «паттерны боли при биомеханических нарушениях суставов краниовертебрального перехода и шейного отдела позвоночника»^[26] или «паттерны двигательных и чувствительных расстройств при патологии нервных структур в дистальных отделах верхней конечности»^[27].

Паттерны широко представлены в глоссарии мануальных терапевтов (например паттерн ходьбы), рефлексотерапевтов (например, паттерн сырости-жара) и прикладных кинезиологов (например, паттерн дыхания).

Паттерны вязания

В вязании часто используются схемы рисунков, которые повторяются через определенное количество столбцов и рядов. Один такой рисунок, предназначенный для многократного повторения в вязаном изделии, и называется паттерном (чаще используют термин раппорт). Паттерн может состоять из различных видов петель, в результате получается объемный узор, или образовываться повторением узора из пряжи различных цветов, например стилизованные цветы или олени на свитерах.

Примечания

1. ↑ Stewart, Ian. 2001. Pages 48-49.
2. ↑ Stewart, Ian. 2001. Pages 64-65.
3. ↑ Stewart, Ian. 2001. Page 52.
4. ↑ Stewart, Ian. 2001. Pages 82-84.
5. ↑ Stewart, Ian. 2001. Page 60.
6. ↑ Stewart, Ian. 2001. Page 71.
7. ↑ Mandelbrot, Benoît B. The fractal geometry of nature. — Macmillan, 1983.
8. ↑ Falconer, Kenneth. Fractal Geometry: Mathematical Foundations and Applications. — John Wiley, 2003.
9. ↑ Briggs, John. Fractals:The Patterns of Chaos. — Thames and Hudson, 1992. — P. 148.
10. ↑ Batty, Michael (1985-04-04). “Fractals – Geometry Between Dimensions”. New Scientist. Holborn Publishing Group. 105 (1450): 31.
11. ↑ Meyer, Yves; Roques, Sylvie. Progress in wavelet analysis and applications: proceedings of the International Conference «Wavelets and Applications,» Toulouse, France – June 1992. — Atlantica Séguier Frontières, 1993. — P. 25.
12. ↑ Carbone, Alessandra; Gromov, Mikhael; Prusinkiewicz, Przemyslaw. Pattern formation in biology, vision and dynamics. — World Scientific, 2000. — P. 78. — ISBN 9789810237929.
13. ↑ Hahn, Horst K.; Georg,Manfred; Peitgen, Heinz-Otto. Fractal aspects of three-dimensional vascular constructive optimization // Fractals in biology and medicine / Losa, Gabriele A.; Nonnenmacher, Theo F.. — Springer, 2005. — P. 55–66.>
14. ↑ Addison, Paul S. Fractals and chaos: an illustrated course. — CRC Press, 1997. — P. 44–46.
15. ↑ Maor, Eli. e: The Story of a Number. Princeton University Press, 2009. Page 135.
16. ↑ Ball, 2009. Shapes pp 29-32.
17. ↑ Kappraff, Jay (2004). “Growth in Plants: A Study in Number” (PDF). Forma. 19: 335—354.
18. ↑ Coxeter, H. S. M. Introduction to geometry. — Wiley, 1961. — P. 169.
19. ↑ Lorenz, Edward N. (March 1963). “Deterministic Nonperiodic Flow”. Journal of the Atmospheric Sciences. 20 (2): 130—141. Bibcode:1963JAtS…20..130L. DOI:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2. ISSN 1520-0469. Проверено 3 June 2010.
20. ↑ Ruelle, David. Chance and Chaos. Princeton University Press, 1991.
21. ↑ Lewalle, Jacques. Flow Separation and Secondary Flow: Section 9.1 // Lecture Notes in Incompressible Fluid Dynamics: Phenomenology, Concepts and Analytical Tools. — Syracuse, NY : Syracuse University, 2006..
22. ↑ Информация из справочника интерьерных идей 4living.ru (неопр.) (недоступная ссылка). Проверено 4 апреля 2013. Архивировано 3 декабря 2012 года.
23. ↑ Ciaccio E. J., Dunn S.M., Akay M. Biosignal pattern recognition and interpretation systems. Part 4 of 4: Review of applications // IEEE Engineering in Medicine and Biology Magazine. — 1994. — Vol. 13, 2006, Issue 2. — P. 269—273.
24. ↑ Гапонова О .В. Электроэнцефалографические паттерны синдрома Веста // Медицинский совет. — 2008.- № 1-2.
25. ↑ Малая меди цинская энциклопедия. — М.: Медицинская энциклопедия. 1991-96 гг.
26. ↑ Небожин А. И., Ситель А. Б. Паттерны боли при биомеханических нарушениях шейного отдела позвоночника // Мануальная терапия. — 2007. — № 1 (25). — С. 2-8.
27. ↑ Паттерны двигательных и чувствительных расстройств при патологии нервных структур в дистальных отделах верхней конечности // Медицинский портал для врачей и студентов doctorspb.ru. 2010. Источник в Интернет: http://doctorspb.ru/articles.php?article_id=1477

ru-wiki.org

Паттерн — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 17 мая 2015; проверки требуют 27 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 17 мая 2015; проверки требуют 27 правок. плитка — пример использования паттернов в дизайне помещений

Па́ттерн (англ. pattern «образец, шаблон; форма, модель; схема, диаграмма») — схема-образ, действующая как посредствующее представление, или чувственное понятие, благодаря которому в режиме одновременности восприятия и мышления выявляются закономерности, как они существуют в природе и обществе.

Паттерн понимается в этом плане как повторяющийся шаблон или образец. Элементы паттерна повторяются предсказуемо. Так, из графических паттернов складываются красивые узоры.

Каждый из органов восприятия (чувств) воспринимает паттерны в соответствии со своими особенностями.

В науке, в том числе в математике и языкознании, паттерны выявляются путём исследования.

Прямое наблюдение может выявлять визуальные паттерны, как они формируются в природе и в искусстве.
Визуальные паттерны в природе часто хаотичны. Они не копируют друг друга и часто являются фрактальными.

Паттерны в природе включают спирали, меандры, волны, пену, трещины, а также паттерны, созданные благодаря симметрии поворота и отражения. Все подобные паттерны имеют математически описываемую структуру, которая может быть выражена формулами, тем не менее математика сама по себе является поиском регулярностей, и любой конечный продукт применения функций является математическим паттерном.

Когда научные теории исследуют и предсказывают синхронно существующие регулярности в природе и обществе, то это и есть выявление паттернов.
В искусстве и архитектуре для получения определенного устойчивого воздействия декорации и различные визуальные элементы могут комбинироваться и повторяться, образуя паттерны.
В компьютерных науках шаблоны проектирования являются широко используемым решением большого класса проблем программирования.

Под паттерном в медицине понимают устойчивую комбинацию результатов исследований или других признаков (например, симптомов) при сходных жалобах пациента или у больных одной нозологии. Понятие «паттерн» включает несколько признаков (симптомов). Синдром включает один или несколько паттернов. Болезнь включает один или несколько синдромов.

Паттерны в природе[ | ]

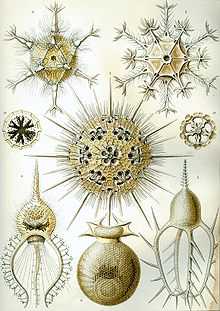рисунки морских животных Эрнста Геккеля, демонстрирующие различные виды симметрии

Ранние греческие философы, такие как Платон, Пифагор, Эмпедокл, исследовали паттерны, пытаясь объяснить порядок в природе. Современное понимание визуальных паттернов формировалось постепенно с развитием наук.

В XIX веке бельгийский физик Жозеф Плато, изучая мыльные пузыри, сформулировал концепцию минимальной поверхности. Немецкий биолог и художник Эрнст Геккель нарисовал сотни морских организмов, подчёркивая их симметрию. Шотландский биолог Дарси Томпсон первым начал изучение паттернов роста как растений, так и животных, показав, что спиральный рост можно описать простыми уравнениями. В XX веке британский математик Алан Тьюринг предсказал механизмы морфогенеза, которые ответственны за образование пятен и полос. Венгерский биолог А

encyclopaedia.bid